Input to the Huffman Compressor will consist of a filename given on the command line. Your main program should open this file for reading, calculate the Huffman Code Table, and print compressed file contents.
Example Run #1
Run with a simple input file.Input File:
Output:
Huffman Code Table:
00003 A: 1
00002 B: 00
00001 C: 01
Compressed File Contents:
A: 1
A: 1
B: 00
A: 1
B: 00
C: 01
Compressed 48 bits into 9 bits.
Compression rate 81%
In this example, the initial Frequency Table will be: [A:3, B:2, C:1], and those frequencies are noted in the leftmost column of the Huffman Code Table above.
When sorted into a priority queue by lowest frequency, the queue will thus be: [C:1, B:2, A:3].
The first step of building the Huffman Tree will dequeue C and B, combining them into a new tree node with total frequency 3. Our reference implementation places the first item dequeued into the right child of the new tree node. When sorted back into the priority queue, the new combined node with frequency 3 will come after the node for A with frequency 3 -- an item inserted with equal frequency will go to the back of the group of equal items: [A:3, Node(B,C):3].
The second step of building the Huffman Tree will dequeue A and the BC node, combining them into a new tree node with total frequency 6. When inserted back into the priority queue, this will become the sole item remaining, and construction of the Huffman Tree is complete.
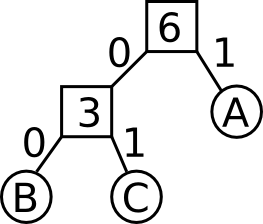
Taking the codes from the tree by reading left branches as '0' and right branches as '1', the final Huffman Code Table has A = 1, B = 00 and C = 01.
The compression figures are calculated by totaling the code length for each letter, and assuming 8 bits per letter in the original encoding.
Example Run #2
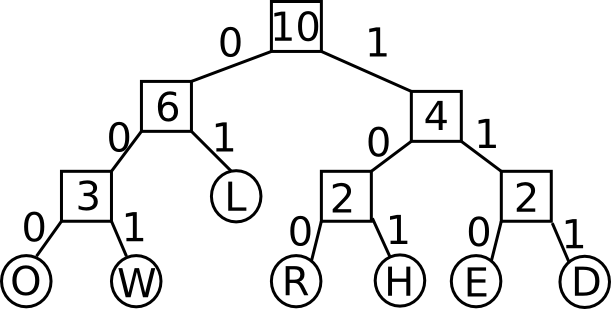
Run with a Hello World input file.Input File:
Output:
Huffman Code Table:
00003 L: 01
00002 O: 000
00001 D: 111
00001 E: 110
00001 H: 101
00001 R: 100
00001 W: 001
Compressed File Contents:
H: 101
E: 110
L: 01
L: 01
O: 000
W: 001
O: 000
R: 100
L: 01
D: 111
Compressed 80 bits into 27 bits.
Compression rate 66%
The priority queue during Huffman Tree construction looks like this:
Step 1. [D:1, E:1, H:1, R:1, W:1, O:2, L:3], dequeue D:1 and E:1
Step 2. [H:1, R:1, W:1, O:2, ED:2, L:3], dequeue H:1 and R:1
Step 3. [W:1, O:2, ED:2, RH:2, L:3] , dequeue W:1 and O:2
Step 4. [ED:2, RH:2, L:3, OW:3], dequeue Node(E,D):2 and Node(R,H):2
Step 5. [L:3, OW:3, RHED:4], dequeue L:3 and Node(O,W):3
Step 6. [RHED:4, OWL:6], dequeue Node(Node(R,H):2, Node(E,D):2):4 and Node(Node(O,W):3, L):6
Step 7. [OWLRHED:10]